| Переглянути всі підручники | |||||||||||||
| << | < | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | > | >> |
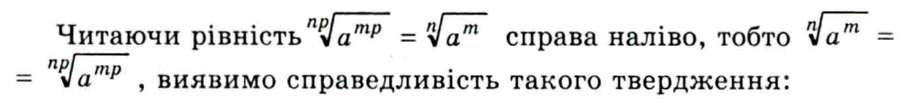
під час множення показника кореня і показника степеня підкореневого виразу на одне й те саме число значення кореня з невід'ємного числа не змінюється.
|
За цим твердженням можна зводити радикали з різними показниками до спільного показника. Наприклад: |
 |
3. Найпростіші перетворення радикалів. Винесення множника за знак радикала. У випадках, коли підкореневий вираз розкладається на множники так, що з одного або з кількох із них можна добути точний корінь, ці множники після добування з них кореня можна записати перед знаком кореня. Таке перетворення називається винесенням множника за знак радикала.
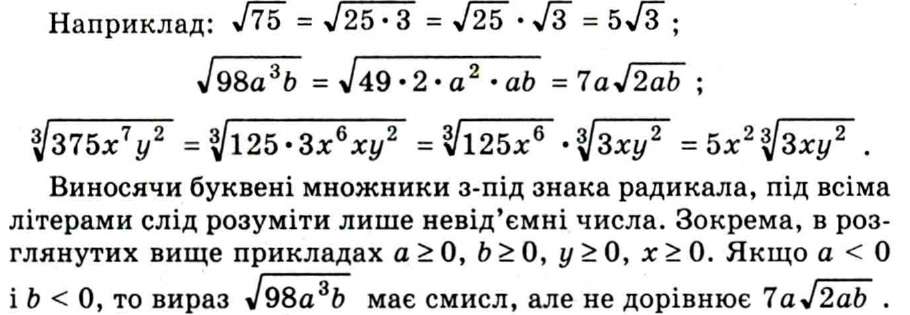 |
|
Щоб дізнатися, з яким показником степеня можна винести за знак кореня множник, а які множники і з якими показниками степенів залишаться під коренем, досить показник степеня множника, що стоїть під коренем, поділити на показник степеня радикала: частка покаже, в якому степені цей множ- |
| Переглянути всі підручники | |||||||||||||
| << | < | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | > | >> |