| Переглянути всі підручники | |||||||||||||
| << | < | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | > | >> |
Під радикал можна вносити як числові, так і буквені множники, тільки треба мати на увазі, що буквений множник не може бути від'ємним.
Зведення радикалів до найпростішого (нормального) вигляду. Вважатимемо, що радикал зведений до найпростішого вигляду, коли: підкореневий вираз не містить дробів; раціональні множники винесені за знак радикала; показник кореня і показник степеня підкореневого виразу скорочені на їх найбільший спільний дільник. Якщо підкореневий вираз є добутком кількох множників, показники степенів яких мають спільний дільник, то показник кореня і показники степенів співмножників поділені на цей дільник.
Наведемо приклади зведення радикалів до найпростішого вигляду:
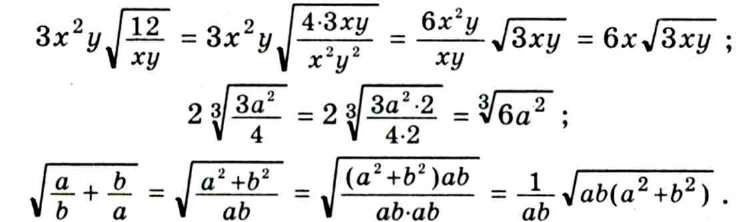
4. Зведення подібних радикалів. Спрощуючи вирази, які містять суму радикалів, користуються перетворенням, що має назву зведення подібних радикалів. Воно аналогічне зведенню подібних членів. Проте означення подібних радикалів відрізняється від означення подібних членів.
Радикали називають подібними, якщо після зведення їх до найпростішого (нормального) вигляду вони мають рівні підкореневі вирази і однакові показники. Наприклад, подібними є радикали:
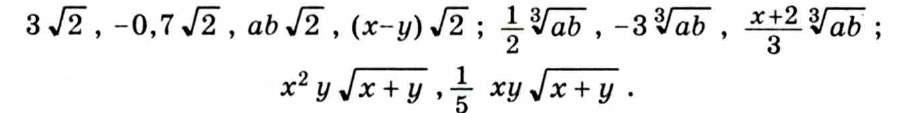
Раціональний множник, що стоїть перед знаком радикала, називають коефіцієнтом.
Якщо радикали не зведені до найпростішого вигляду, то не можна казати про їх подібність. Щоб це з'ясувати, слід їх спростити, тобто: звільнитися під радикалом від дробів; винести за знак радикала ті множники, з яких добувається точний корінь; показники кореня і степеня підкореневого виразу скоротити на найбільший спільний дільник.
Розглянемо приклади на доведення подібності радикалів.
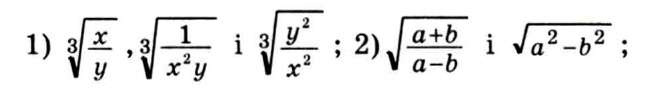
| Переглянути всі підручники | |||||||||||||
| << | < | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | > | >> |