| Переглянути всі підручники | |||||||||||||
| << | < | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | > | >> |
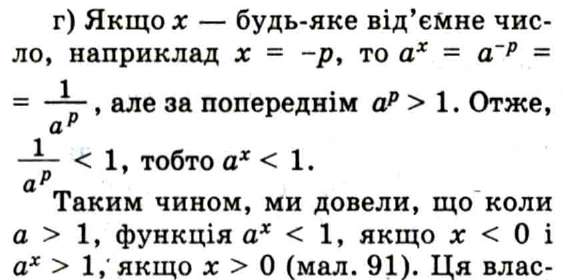
тивість дає змогу встановити, в яких частинах координатної площини буде розміщений графік функції у = ах, якщо а > 1 (на мал. 92 ці частини заштриховано).
Нехай 0 < а < 1.
1. Якщо 0 < а < 1, функція ах при зростанні х монотонно спадає (мал. 93).
2. Якщо 0 < а < 1, функція у = ах при необмеженому зростанні показника х набуває значень як завгодно близьких до нуля, а при необмеженому спаданні показника х функція необмежено зростає.
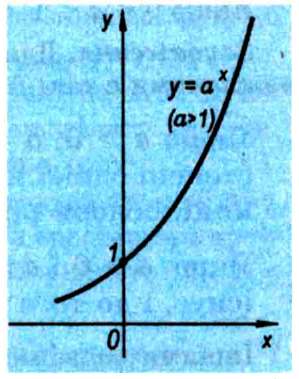
3. Якщо 0 < а < 1, то показникова функція ах більша за 1 для всіх від'ємних значень х і менша за 1 для всіх додатних значень х, тобто ах > 1 для х < 0 і ах < 1 для х > 0. Справедливість цих тверджень випливає з того, що значення показникової функції з основою, меншою від 1, обернені до відповідних значень показникової функції з основою, більшою від 1:
 |
|
Мал. 91 |
 |
|
Мал. 92 Мал. 93 |
| Переглянути всі підручники | |||||||||||||
| << | < | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | > | >> |