| Переглянути всі підручники | |||||||||||||
| << | < | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | > | >> |
Складання рівняння задачі є основним засобом застосування математики до природознавства і техніки. Без рівняння немає математики як засобу пізнання природи.
П. С. Александров
§11. Обернені тригонометричні функції
Поняття про обернену функцію. Під час розв'язування різних задач часто доводиться обчислювати значення функції за даним значенням аргументу. Наприклад, обчислювати площу S квадрата за довжиною його сторони за формулою S = а2, яка задає залежність (функцію) площі від довжини а сторони квадрата. Проте часто доводиться розв'язувати обернену задачу: якою має бути сторона квадрата а, щоб площа S мала напе-

Розглянемо приклади знаходження функцій, обернених до лінійної у = kx + Ь і квадратичної у = х2 функцій.
Приклад 1. Нехай у = 2х + 3 = f(x) — задана лінійна функція. Областю визначення і областю значень її є множина всіх дійсних чисел. Кожне своє значення у лінійна функція набуває лише при одному значенні аргументу д:.
Вважатимемо змінну у незалежною (аргументом), а змінну х — залежною і розв'яжемо рівняння у = 2х + 3 відносно змінної х. Дістанемо також лінійну функцію яка задає іншу залежність х від у.

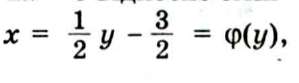
| Переглянути всі підручники | |||||||||||||
| << | < | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | > | >> |