| Переглянути всі підручники | |||||||||||||
| << | < | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | > | >> |
Нехай треба, наприклад, помножити 64 на 512. Знайдемо логарифм цього добутку за основою 2. Маємо log2(64 • 512) =log264 + log2512. За таблицею знаходимо log264 = 6, log2512 = 9. Отже, log2(64 • 512) ==6 + 9=15. Але числу 15 з першого рядка відповідає число 32 768 з другого рядка. Отже, 64.512= 32 768.
Застосовуючи теорему про логарифм частки (дробу), можна скористатися таблицею і під час ділення чисел.
Наприклад, треба поділити 8192 на 128. Знайдемо логарифм цієї частки за основою 2. Маємо:

Джон НЕПЕР
(1550—1617)
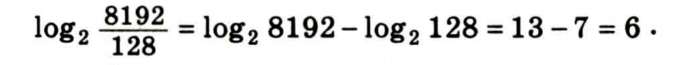
Але числу 6 першого рядка відповідає число 64 другого рядка. Отже: 8192 : 128 = 64.
Можна скористатися таблицею і для піднесення чисел до степеня. Наприклад, обчислимо 45. Маємо: log245 = 5log24 = = 5 • 2 = 10. Числу 10 першого рядка таблиці відповідає число 1024 другого рядка. Отже, 45 = 1024.
Як бачимо, дії другого ступеня (множення, ділення) звелися до дій першого ступеня (додавання, віднімання) над відповідними логарифмами. При цьому довелося виконувати дії із значно меншими числами.
Для практичного здійснення ідеї Штіфеля треба було скласти геометричну прогресію, яка зростала б дуже повільно, бо лише при цьому вона може охоплювати значну кількість чисел. Бюргі взяв знаменником прогресії число 1,0001 замість 2, як було у Штіфеля.
Пізніше основою таблиць почали називати той член, якому в арифметичній прогресії відповідає число 1. У Бюргі основою був 10 001-й член геометричної прогресії, тобто 1,000110000,
або (1 + 10-4 )10 = 2,71814593 (в арифметичній прогресії йому відповідало число 0,0001 • 104 = 1).
Бюргі прийшов до логарифмів раніше, ніж Непер, але опублікував свої таблиці лише у 1620 р. Таким чином, першою в 1614 р. з'явилася праця Непера «Описання дивовижної таблиці логарифмів». Основою таблиці логарифмів Непера є ірраціональне число, до якого необмежено наближаються числа
| Переглянути всі підручники | |||||||||||||
| << | < | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | > | >> |