| Переглянути всі підручники | |||||||||||||
| << | < | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | > | >> |
Систематизуємо властивості логарифмів, які слід запам'ятати, щоб упевнено використовувати їх під час розв'язування різноманітних вправ, виконання практичних розрахунків. Спільні властивості для випадків а>1і0<а<1:
будь-яке додатне число має логарифм і до того ж тільки один;
від'ємні числа і число 0 не мають логарифмів; логарифм одиниці дорівнює нулю; логарифм основи дорівнює одиниці.
Властивості логарифмів чисел за основою а > 1: якщо iVj > N2, то і loga N1 > logа N2, тобто більше число має більший логарифм, і навпаки;
логарифми чисел, більших за 1, додатні; логарифми чисел, менших за 1, від'ємні;
якщо число зростає необмежено, то і логарифм його зростає необмежено;
якщо число, залишаючись додатним, прямує до нуля, то логарифм його стає від'ємним і як завгодно великим за модулем. Властивості логарифмів чисел за основою 0 < a < 1: якщо Ni > N2,то loga N1 < loga N2, тобто більше число має менший логарифм;
логарифми чисел, більших за 1, від'ємні; логарифми чисел, менших за 1, додатні;
якщо число зростає необмежено, то його логарифм спадає
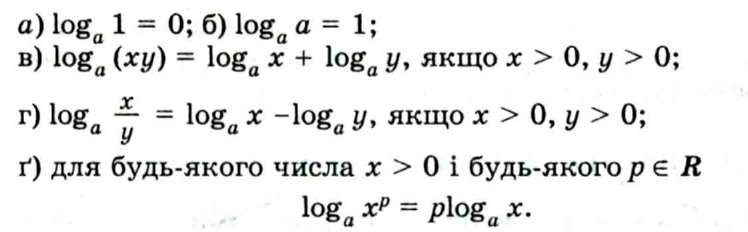 |
|
Для порівняння наведемо властивості показникової і логарифмічної функцій у вигляді таблиці (табл. 8). |
Таблиця 8

| Переглянути всі підручники | |||||||||||||
| << | < | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | > | >> |