| Переглянути всі підручники | |||||||||||||
| << | < | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | > | >> |
 |
|
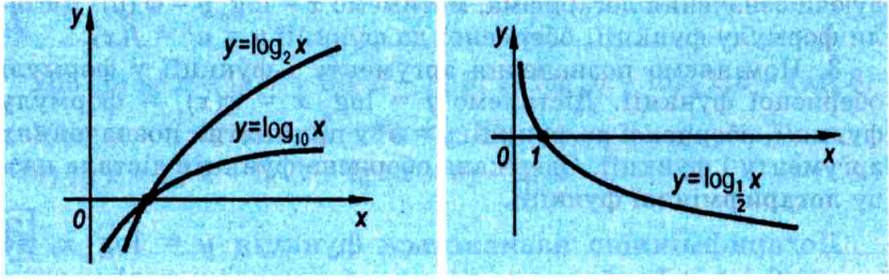
Мал. 100 |
|
Мал. 99 |
 |
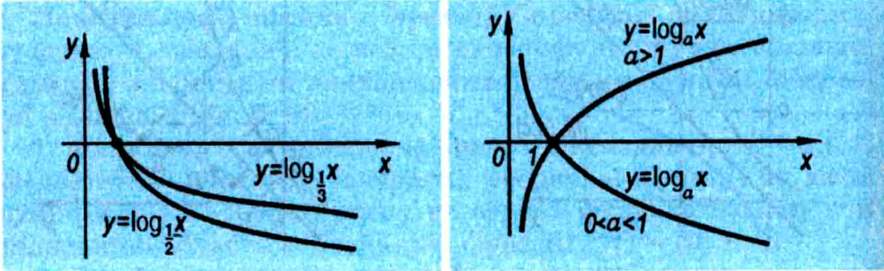
Властивості логарифмічної функції. Знаючи властивості взаємно обернених функцій, можна легко дістати властивості логарифмічної функції з показникової. Характер графіка показникової функції за основою а залежить від того, буде а > 1 чи 0 < а < 1. Тому і характер графіка логарифмічної функції за основою а залежить від тих самих умов. Отже, для функції у = loga д: слід розрізняти 2 випадки: a>li0<a<l (мал. 102). У кожному з них властивості логарифмічної функції випливають із властивостей показникової, якщо врахувати ще зв'язок між графіками показникової й логарифмічної функцій (див. табл. 8). Отже, маємо такі властивості логарифмічної функції.
1) Область визначення логарифмічної функції — множина всіх додатних чисел.
2) Область значень логарифмічної функції — множина всіх дійсних чисел.

 |
|
Мал. 101 Мал. 102 |
| Переглянути всі підручники | |||||||||||||
| << | < | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | > | >> |