| Переглянути всі підручники | |||||||||||||
| << | < | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | > | >> |
Основоположне поняття математичного аналізу — це поняття функціональної залежності, в якому, як у зародку, вже закладена вся ідея оволодіння явищами природи і процесами техніки за допомогою математичного апарату.
О. Я. Хінчин
§ 16. Корінь п-го степеня та його властивості
1. Поняття кореня n-го степеня. В курсі алгебри 8-го класу було введено поняття квадратного кореня.
Квадратним коренем з числа а називають число, квадрат якого дорівнює а.

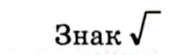

Квадратний корінь з 0 дорівнює 0, бо 02 = 0. Цей корінь з 0 єдиний. Квадратний корінь з -25 не існує, бо немає такого числа, квадрат якого дорівнював би -25.
Отже, квадратних коренів з додатного числа існує два: один додатний, а другий від'ємний.
Додатний квадратний корінь з додатного числа а називають арифметичним квадратним коренем і позна-
називають знаком арифметичного кореня; вираз, що стоїть під знаком кореня, називається підкореневим виразом.
Додатні числа разом з числом нуль називають невід'ємними числами. Надалі поняття арифметичного квадратного кореня будемо вживати для невід'ємних чисел.

| Переглянути всі підручники | |||||||||||||
| << | < | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | > | >> |