| Переглянути всі підручники | |||||||||||||
| << | < | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | > | >> |
Наслідок.
Логарифм дробу, чисельник якого дорівнює одиниці, дорівнює логарифму знаменника, взятому з протилежним знаком.
(Обґрунтуйте це твердження самостійно. Можна також довести теорему 2, користуючись основною логарифмічною тотожністю.)
Теорема 3.
Логарифм степеня додатного числа дорівнює показнику степеня, помноженому на логарифм основи цього степеня, тобто

 |
|
Теорема 4. |
Логарифм кореня з додатного числа дорівнює логарифму підкореневого виразу, поділеному на показник кореня, тобто
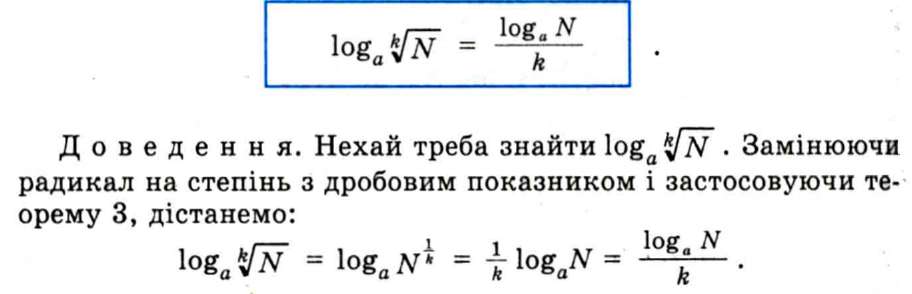
Теорема 5.
Якщо логарифми двох додатних чисел за тією самою основою рівні, то й самі числа рівні. І навпаки, якщо два додатні числа рівні, то і їх логарифми за тією самою основою рівні.
| Переглянути всі підручники | |||||||||||||
| << | < | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | > | >> |