| Переглянути всі підручники | |||||||||||||
| << | < | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | > | >> |
§18. Узагальнення поняття степеня. Степенева функція
|
Степінь з натуральним і цілим показником. Для узагальнення поняття степеня нагадаємо основні поняття і формули. |
 |
Іноді цю рівність необхідно прочитати справа наліво: щоб помножити степені з однаковими показниками, достатньо перемножити основи і результат піднести до степеня з тим самим показником: аn bn сn = (abc)n.
Щоб піднести до степеня дріб, треба піднести до цього степеня чисельник і знаменник і перший результат поділити на другий:
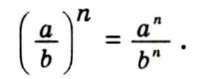
Щоб піднести до степеня степінь, треба показники степенів перемножити, а основу степеня залишити без зміни: (ат)п = атп.
Зазначимо, що у формулюванні цих правил ніде не вказувалося, яким має бути показник степеня: натуральним числом чи цілим. Це тому, що множина цілих чисел включає множину натуральних чисел як свою частину. Отже, наведені правила стосуються степенів з натуральним, нульовим і цілим від'ємним показниками. Зрозуміло, що для випадку степеня з нульовим і цілим показниками ставиться додаткова умова, щоб основа степеня не дорівнювала нулю.
Степінь з раціональним показником. Введення степеня з нульовим і від'ємним показниками було першим розширенням поняття про степінь. При цьому нові означення степеня з нульовим і від'ємним показниками було введено так, що властивості степеня з натуральним показником залишилися правильними і для степенів з цілим показником.
| Переглянути всі підручники | |||||||||||||
| << | < | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | > | >> |